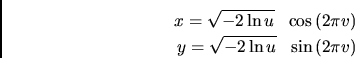Cómo obtener un generador de números aleatorios

Este apendice trata de explicar cómo obtener un generador de números aleatorios que responda a una distribución conocida a partir de una uniforme.

Casi todos los ordenadores y lenguajes de programación, poseen un generador intrínseco de números pseudo-aleatorios uniformes en el intervalo 0, 1. Quisiéramos pues, aprovechar este generador para obtener números aleatorios que sigan otra distribución.

Sea $f(x)$ la densidad de probabilidad que queremos generar y $F(x)$ su función de distribucion, definida como:

\begin{displaymath} F(x) = \int_a^x f(x) dx \end{displaymath}

(donde a es el origen inferior en el que está definido f(x), por ejemplo, para una gaussiana $a=-\infty$).

Se puede demostrar que la variable aleatoria $r$ definida como:

\begin{displaymath} r = F(x) \end{displaymath}

está distribuida uniformemente. Esta propiedad puede usarse para obtener nuestro generador.

Para obtener un número aleatorio que siga nuestra distribución, llamaremos al generador de nuestro ordenador que nos proporcionará un número r. Calcularemos $ x = F^{-1}(r) $ , y ya tenemos el número que buscamos.

EJEMPLO

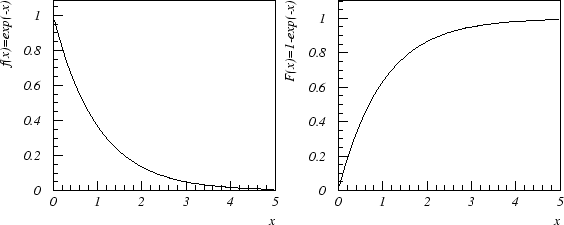
Supongamos que queremos un generador con $f(x)=exp(-x)$.

Figura 1: Ejemplo
\begin{figure} \begin{center} \setlength{\unitlength}{1cm} \begin{picture}... ...fxsize =14cm \epsffile{f_exam.eps}\end{picture} \end{center} \end{figure}

1)
Calculemos:

\begin{displaymath} F(x) = \int_0^x f(x) dx = \int_0^x e^{-x} dx = 1 - e^{-x} \end{displaymath}

2)
Lo igualamos al número aleatorio uniforme

\begin{displaymath} r = 1 - e^{-x} ~~~~~ \Rightarrow ~~~~~ x = -\ln{(1-r)} \end{displaymath}

3)
Para obtener números aleatorios $x$, llamamos a nuestro generador uniforme y calculamos $x$ con la fórmula anterior.
Generador de números gaussianos

Queremos ahora generar números aleatorios distribuidos según una gaussiana de media 0 y sigma 1. Podríamos intentar aplicar el método anterior, pero fracasaríamos ya que la gaussiana no es integrable analíticamente y por lo tanto no podríamos obtener una fórmula para $F(x)$. Sin embargo existen otras técnicas que no explicaremos en detalle.

Damos a continuación un método práctico para obtenerlos:

1)
Obtener dos números aleatorios de una distribución uniforme $u$ y $v$
2)
Calcular:

\begin{eqnarray*} x = \sqrt{ -2 \ln{u} } ~~\cos{(2\pi v)} \\ y = \sqrt{ -2 \ln{u} } ~~\sin{(2\pi v)} \end{eqnarray*}



3)
$x$ e $y$ así calculados son dos números aleatorios independientes que siguen una distribución gaussiana (de media 0, varianza 1)
Este método es exacto y fácil de programar, pero tiene la desventaja de que no es muy rápido debido al cálculo del logaritmo, seno y coseno.

El siguiente algoritmo es una mejora a este método:

1)
Generar dos números aleatorios uniformes $u$ y $v$
2)
Calcular $w = (2u-1)^2 + (2v-1)^2$
3)
Si $w>1$ ir a 1)
4)
Devolver $x=uz$ e $y=vz$, con $z=\sqrt{-2\ln{w}/w}$

Esta variación elimina el seno y el coseno a expensas de un rechazo del $\approx 21\%$ en el paso 3.


Este guión ha sido basado en el trabajo previo realizado por el grupo de Altas Energías del departamento de Física Atómica, Molecular y Nuclear. Agradecimientos a José Luis Contreras y Abelardo Moralejo. Enlaces útiles para hacer las prácticas 2001-10-16

-------------------------------------------------------------------------------------------------------------------------------------