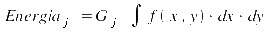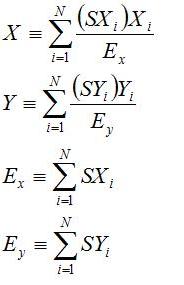PRÁCTICA

IDENTIFICACIÓN DEL CRISTAL DE INTERACCIÓN EN ESCÁNERES PET DE ALTA RESOLUCIÓN

1- OBJETIVOS DE LA PRÁCTICA

Esta práctica tiene como objetivo el estudio y la comparación de los resultados obtenidos en una simulación de un escáner PET con los resultados reales obtenidos con ese mismo escáner. Para ello, nos centraremos en los siguientes puntos:

1- Resolución en energía.

2- Identificación del cristal de interacción mediante lógica de Anger.

En la segunda parte de la práctica veremos como varían estos resultados cuando variamos el tiempo de integración del sistema electrónico.

2- RESOLUCIÓN EN ENERGÍA

La resolución en energía de un sistema para una energía dada viene determinada por la distribución del fotopico para un espectro medido por dicho sistema con un haz monoenergético. El parámetro que se toma como referencia para ello es la anchura a mitad de altura en el fotopico del espectro medido (FWHM).

En PET los fotones incidentes son monoenergéticos, (511 keV), por eso en este caso una buena resolución en energía no sólo es necesaria para diferenciar estos fotones de otros de distintas energías que introduciran ruido en las mediciones, sino que debido a que los detectores PET son de pequeño tamaño para conseguir una gran resolución espacial, muchos fotones de 511 keV no depositan toda su energía en los cristales centelleadores.

3- DISTRIBUCIÓN ESPACIAL DE LOS FOTONES

Los fotones que salen de un cristal iluminan un área del fotomultiplicador mayor que la sección del cristal debido a un ensanchamiento en la distribución espacial de los fotones en su propagación desde que salen del cristal, pasan por el pegamento óptico, la ventana del PMT y llegan finalmente al fotocátodo.

Este ensanchamiento de los fotones en la interfaz se simula en la práctica mediante una distribución aproximadamente de cola Gaussiana.

La energía recogida por cada ánodo j se puede calcular integrando la distribución espacial de los fotones que salen del centelleador entre las dimensiones de cada ánodo:

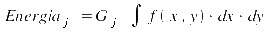
Donde G_j es la ganancia de cada ánodo y f (x,y) es la distribución espacial de los fotones tras salir del centelleador.

4- LÓGICA DE ANGER

La lógica de Anger se utiliza para calcular la posición de interacción entre el rayo gamma y el cristal utilizando fotomultiplicadores multiánodo.

Cuando un rayo gamma llega al centelleador, este puede sufrir varias interacciones en un cristal o en varios:

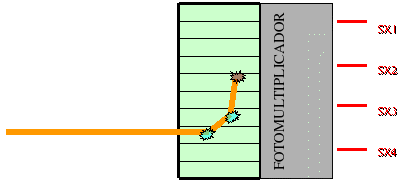
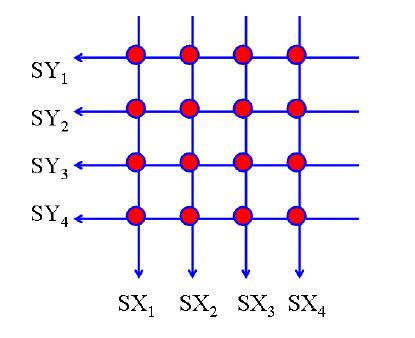
La lógica de Anger consiste en sumar todas las señales Sx y todas las Sy para hacer una media ponderada y obtener así un punto (x,y) que dará una idea de la posición inicial de interacción del rayo gamma con el centelleador.

Una vez obtenidos los puntos (x,y) de Anger, dividimos la superficie del fotomultiplicador (52 x 52 mm) en una malla de 256 x 256 bines; y vamos asignando a cada suceso uno de estos bines; obteniendo el resultado de la siguiente figura (imagen de llenado de campo):

Tanto en el caso real como en la simulación se distinguen solo 28 x 28 cristales; puesto que los cristales de los extremos presentan una mayor dispersión de luz y no es posible distinguirlos.

5- APILAMIENTO (pile-up)

Cuando un fotón interacciona en un detector la electrónica comienza un periodo predefinido durante el cual se integra toda la intensidad que es depositada en el mismo. Este periodo de tiempo se conoce como tiempo de integración.

Si dos o más fotones interaccionan en un mismo detector en un periodo de tiempo inferior al tiempo de integración la electrónica es incapaz de diferenciar la llegada de los distintos pulsos y se produce un apilamiento o suma de las señales (pile-up). Esto tiene como consecuencia que la electrónica detecte un sólo evento cuya energía es la depositada por los dos fotones.

Esto dá lugar a una distorsión en el espectro energético y a una consiguiente pérdida de eventos. Interesa eliminar los eventos que sufren pile-up debido a que el posicionamiento espacial difiere mucho de las posiciones de interacción iniciales, con la consecuente pérdida de resolución espacial que ello conlleva.

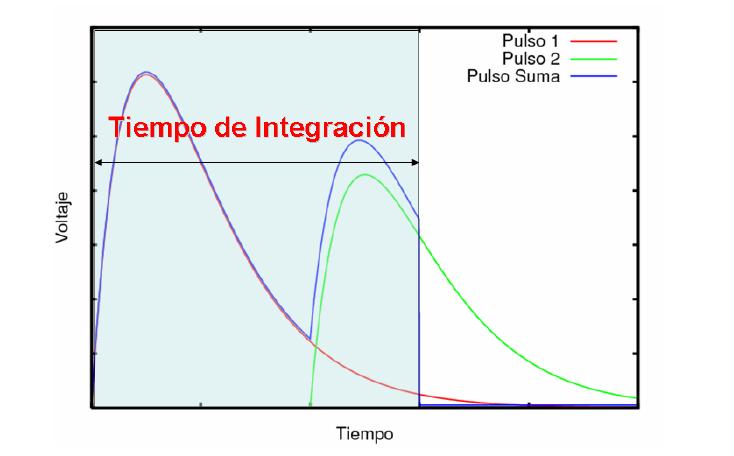
Representación de una señal en la que se produce pile-up debido a la llegada de un segundo pulso en el tiempo de integración

El tiempo de integración que usaremos inicialmente en la simulación de esta práctica es de 200 ns.

6 – RESULTADOS EXPERIMENTALES

6.1- Espectros de energía: Se trata de obtener los espectros de energía tanto de la simulación como del caso real a partir de los datos presentes en los archivos adjuntos. A partir de la representación gráfica de estos datos, identificar el rango de energías en el que los fotones son dispersados por efecto Compton, los fotones que interaccionan mediante efecto fotoeléctrico, y los eventos que han sufrido pile-up.

Estimar el FWHM para ambos casos y comentar los resultados.

6.2- Lógica de Anger: A partir de los perfiles transversales de una imagen de llenado de campo similar a la mostrada en el apartado 4; estudiaremos la relación pico-valle tanto para una adquisición real como para la simulación.

6.3- Reducción del tiempo de integración: A continuación se presentan los datos correspondientes a los espectros de energía y los perfiles transversales de una imagen de llenado de campo simulados para tiempos de integración de 100, 80 y 50 ns.

Con estos datos repetir los apartados 6.1 y 6.2; y comentar las diferencias que surgen respecto al caso de la simulación con 200 ns (caso inicial) y respecto a la adquisición real.

Espectros de energía simulados	Perfiles transversales de los llenados de campo simulados
Espectro_t-integ = 100 ns	Perfil_t-integ = 100 ns
Espectro_t-integ = 80 ns	Perfil_t-integ = 80 ns
Espectro_t-integ = 50 ns	Perfil_t-integ = 50 ns