|
Aniquilación de un par e+- e- |
Figura 1. Desintegración del par electrón-positrón
Cuando un
positrón atraviesa la materia experimenta
distintos procesos de interacción con el medio, es decir, sufre procesos de excitación e ionización
de átomos y disminuye su velocidad hasta alcanzar energías térmicas (~kB T, donde kB es la constante
de Boltzmann y T la temperatura)
en un proceso de termalización de unos pocos picosegundos.
Una vez que los positrones han alcanzado el equilibrio térmico con el medio,
tiene lugar el proceso de difusión, durante el cual el positrón interactúa con
los alrededores y se aniquila con un electrón.
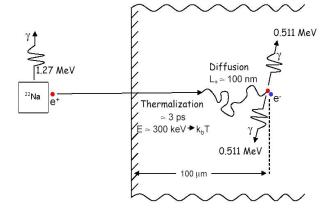
Figura 2. El positrón
procedente de la fuente penetra en la muestra donde experimenta los procesos de termalización y difusión para acabar aniquilándose con el
electrón.
La aniquilación
del par (e-, e+) sólo es posible si se cumplen las leyes de conservación del
momento y la energía, que para el caso de dos fotones de aniquilación tienen la
forma:
En estas expresiones,
,
donde m0 es la masa en
reposo del electrón, k1 y k2 los momentos de
ambos fotones, E la energía del
par electrón- positrón y v la velocidad del
centro de masas del par en el sistema de referencia de
laboratorio.
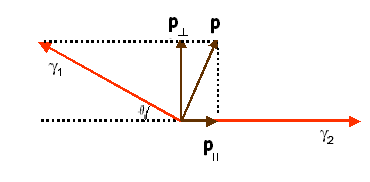
Figura
3.
Esquema de los momentos en el proceso de la aniquilación con emisión de dos
rayos gamma .
Según las
ecuaciones (1) y (2), si el centro de masas del par en el sistema de
laboratorio, está fijo (
), los dos fotones de aniquilación salen en
direcciones opuestas (el ángulo
) y con la misma energía, igual a la mitad
de la energía total del sistema:
En el sistema
de laboratorio, debido al movimiento del par electrón-positrón (
) los dos fotones se desvían ligeramente de la colinealidad
y sus energías difieren de 0.51
MeV.
Si, como suele
ser el caso, el momento del par en el momento de la aniquilación es tal que
, el ángulo de desviación viene dado por:
donde 
es la
componente del momento del par electrón-positrón transversal a la dirección de
emisión de los fotones.
De igual forma, el movimiento
del par causa un ensanchamiento Doppler en la energía de los fotones de
aniquilación dado por:
donde 
es la
componente del momento del par electrón-positrón en la dirección de emisión de
los fotones.
Dado que la
energía de los positrones termalizados es muy pequeña (~kBT), los valores de 
y 
están
relacionados con los momentos de los electrones del sólido. Como consecuencia,
la anchura y la forma de la línea de aniquilación contienen información sobre
los electrones con los que el positrón se aniquila.